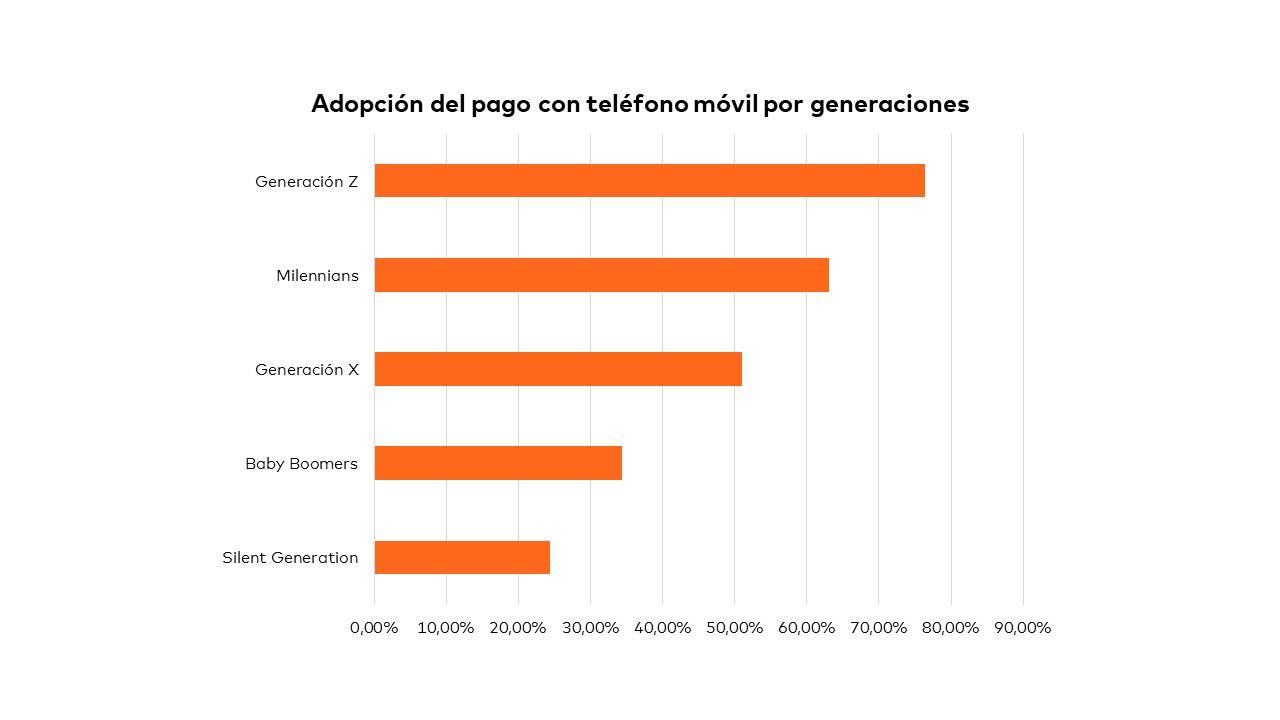
¿Por qué pueden utilizarse las curvas elípticas para cifrar?

En 1987, Neal Koblitz y Victor Miller propusieron de forma independiente utilizar curvas elípticas  sobre cuerpos finitos para implementar algunos criptosistemas ya existentes, lo que se conoce como Criptografía de Curva Elíptica o ECC (Elliptic Curve Cryptography).

La ventaja que ofrece esta nueva criptografía es que se pueden emplear claves más pequeñas que las utilizadas en otros criptosistemas muy extendidos como el RSA y ElGamal, manteniendo la misma seguridad. Para analizar tanto el funcionamiento como la seguridad de esos criptosistemas, antes es preciso comprender qué son las curvas elípticas, y por qué pueden aplicarse al campo de la Criptografía.

Es posible sumar dos puntos de una curva elíptica obteniendo como resultado otro punto de la curva mediante las fórmulas adecuadas, aunque también se puede interpretar gráficamente por el método de la cuerda y tangente. En la figura, el punto R es el resultado de sumar los puntos P y Q. Este punto suma se determina trazando la cuerda que pasa por los puntos P y Q, luego se considera el tercer punto de corte de la curva, es decir -R, y se toma como resultado el punto de la curva simétrico de este último.

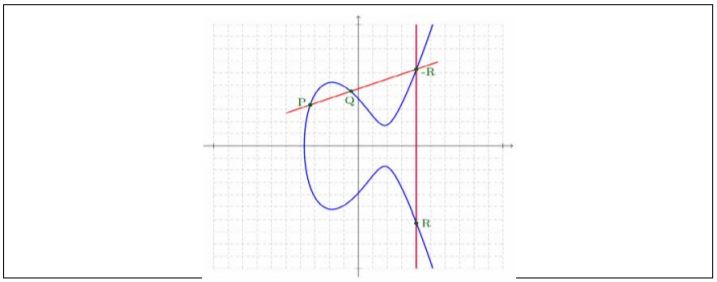
Ahora bien, en criptografía no se utilizan las curvas debido a los errores de redondeo asociados a los números reales, al ser utilizados en computadoras, sino que se utilizan curvas elípticas definidas sobre cuerpos finitos. Este hecho se traduce en que las curvas tienen un número finito de puntos cuyas coordenadas son números enteros. Esta característica es de extrema importancia para poder realizar cálculos con los puntos de modo eficiente y sin errores de redondeo.

En la práctica, se consideran dos tipos de cuerpos finitos para las curvas elípticas en criptografía: los cuerpos primos F_p, que tienen un número primo de elementos, y los cuerpos binarios F₂ ^m, cuyo número de elementos es una potencia prima de dos. El siguiente vídeo ilustra el concepto, y forma parte de la biblioteca del proyecto Thoth.

Autores del guión: Víctor Gayoso Martínez y Luis Hernández Encinas
Dirección Proyecto Thoth: Jorge Ramió Aguirre, Alfonso Muñoz Muñoz

Jorge Ramió Aguirre Doctor por la Universidad de León, Sistemas Inteligentes en la Ingeniería. Profesor en el Departamento de Sistemas Informáticos - ETSISI de la Universidad Politécnica de Madrid. Premio 2015 al Conocimiento de ISACA Madrid.